JAVA中的线程安全与非线程安全
再说什么是线程安全之前我们先来聊聊什么是进程。
1、什么是进程?
先来看一张图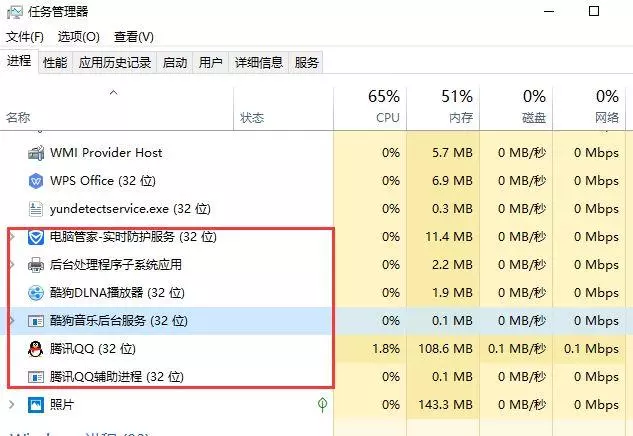
我们看到的这些单独运行的程序就是一个独立的进程,进程之间是相互独立存在的。
我们上面图中的QQ、酷狗播放器、电脑管家等等都是独立的进程。
2、什么是线程?
上面简单的说了一下什么是进程,进程想要执行任务需要依赖线程,换句话说就是进程中的最小执行单位就是线程,并且一个进程中至少有一个线程。
3、什么是多线程?
提到多线程这里要说两个概念,就是串行和并行,搞清楚这个我们才能更好的理解多线程。
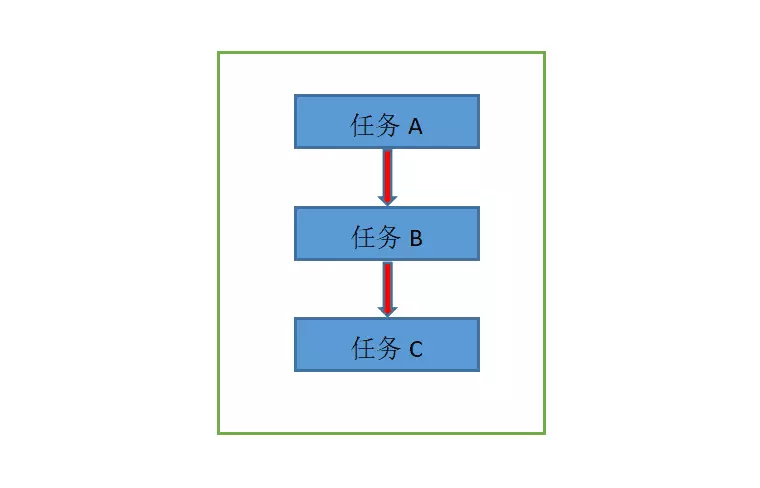
- 串行:其实是相对于单条线程来执行多个任务来说的,我们就拿下载文件来举个例子,我们下载多个文件,在串行中它是按照一定的顺序去进行下载的,也就是说必须等下载完A之后,才能开始下载B,它们在时间上是不可能发生重叠的。
- 并行:下载多个文件,开启多条线程,多个文件同时进行下载,这里是严格意义上的在同一时刻发生的,并行在时间上是重叠的。
4、线程安全
线程安全就是多线程访问时,采用了加锁机制,当一个线程访问该类的某个数据时,进行保护,其他线程不能进行访问直到该线程读取完,其他线程才可使用。不会出现数据不一致或者数据污染。
5、线程不安全
就是不提供数据访问保护,有可能出现多个线程先后更改数据造成所得到的数据是脏数据
ArrayList和Vector有什么区别?HashMap和HashTable有什么区别?StringBuilder和StringBuffer有什么区别?这些都是Java面试中常见的基础问题。面对这样的问题,回答是:ArrayList是非线程安全的,Vector是线程安全的;HashMap是非线程安全的,HashTable是线程安全的;StringBuilder是非线程安全的,StringBuffer是线程安全的。因为这是昨晚刚背的《Java面试题大全》上面写的。此时如果继续问:什么是线程安全?线程安全和非线程安全有什么区别?分别在什么情况下使用?这样一连串的问题,一口老血就喷出来了…
二者如何取舍
非线程安全是指多线程操作同一个对象可能会出现问题。而线程安全则是多线程操作同一个对象不会有问题。
线程安全必须要使用很多synchronized关键字来同步控制,所以必然会导致性能的降低。
所以在使用的时候,如果是多个线程操作同一个对象,那么使用线程安全的Vector;否则,就使用效率更高的ArrayList。
非线程安全!=不安全
有人在使用过程中有一个不正确的观点:我的程序是多线程的,不能使用ArrayList要使用Vector,这样才安全。
非线程安全并不是多线程环境下就不能使用。注意我上面有说到:多线程操作同一个对象。注意是同一个对象。比如最上面那个模拟,就是在主线程中new的一个ArrayList然后多个线程操作同一个ArrayList对象。
如果是每个线程中new一个ArrayList,而这个ArrayList只在这一个线程中使用,那么肯定是没问题的。
线程安全的实现
线程安全是通过线程同步控制来实现的,也就是synchronized关键字。
class Counter
{
private int count = 0;
public int getCount()
{
return count;
}
public synchronized void addCount()
{
count++;
}
}